|
|
|
|
|
|
|
|
|
|
|
|
|
|
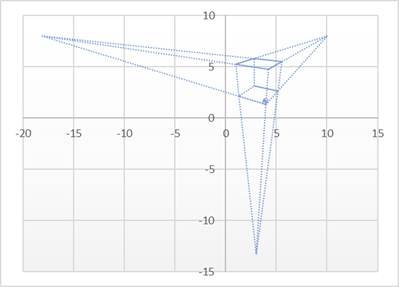
Abbildung aus Perspektive eines
Beobachters auf eine Mattscheibe (xy) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Beispiel: |
P0abc = |
( |
1 |
1 |
1 |
)T |
|
|

|
|
|
Parameter: |
Nxyz = |
( |
3 |
1 |
20 |
)T |
|
|
BH = |
10 |
|
|
|
|
φa = φb = |
30° |
-(0,52 RAD) |
Drehung abc über c |
|
|
φc = |
35° |
(0,61 RAD) |
Drehung abc über b |
|
|
b"/x = |
-1 |
|
Größenverhältnis b' zu x |
|
|
c"/y = |
1 |
|
Größenverhältnis c' zu y |
|
|
a"/z = |
1 |
|
Größenverhältnis a' zu z |
|
|
|
Bxyz = |
( |
3 |
1 |
-10 |
)T |
|
|
Hxyz = |
( |
3 |
1 |
0 |
)T |
|
|
B, H und N liegen auf einer Linie,
die xy in H rechtwinklig schneidet. |
|
|
|
Rotation: |
|
( |
cos φa |
- sin φa |
0 |
) |
|
|
Mφa = |
( |
sin φa |
cos φa |
0 |
) |
|
|
( |
0 |
0 |
1 |
) |
|
|
|
|
( |
0,8660254 |
0,5 |
0 |
) |
|
|
= |
( |
-0,5 |
0,8660254 |
0 |
) |
|
|
( |
0 |
0 |
1 |
) |
|
|
|
P0a'b'c = |
( |
1,3660254 |
0,3660254 |
1 |
)T |
|
|
|
( |
cos φc |
0 |
- sin φc |
) |
|
|
Mφc = |
( |
0 |
1 |
0 |
) |
|
|
( |
sin φc |
0 |
cos φc |
) |
|
|
|
|
( |
0,81915204 |
0 |
-0,5735764 |
) |
|
|
= |
( |
0 |
1 |
0 |
) |
|
|
( |
0,57357644 |
0 |
0,81915204 |
) |
|
|
|
P0a"b"c" = |
( |
0,54540607 |
0,3660254 |
1,60267203 |
)T |
|
|
|
= Mφc * Mφa * P0abc |
|
|
|
= Punkt bezogen auf
Koordinatensystem a"b"c", das parallel zu xyz ist |
|
|
|
Längenkorrektur und Verschieben: |
|
|
P0xyz = |
( |
b"/(b"/x)+Nx |
c"/(c"/y)+Ny |
a"/(a"/z)+Nz |
)T |
|
|
|
= |
( |
2,6 |
2,6 |
20,5 |
)T |
|
|
|
Projektion: |
|
|
P'Hx / BH = |
Px / (BH + Pz) |
ebenso für y statt x |
|
|
|
P' = |
( |
Px / (BH + Pz) * BH + Hx |
Py / (BH + Pz) * BH + Hy |
0 |
)T |
|
|
|
P'0xyz = |
( |
3,9 |
1,9 |
0 |
)T |
|
|
|
Fluchtpunkte: |
|
|
Ein erstaunliches Ergebnis ist, dass
die Parallelen der Achsen sich optisch in je einem Punkt schneiden. |
|
|
|
a*xy = |
( |
10,0 |
8,0 |
)T |
|
|
b*xy = |
( |
-18,1 |
8,0 |
)T |
|
|
c*xy = |
( |
3,0 |
-13,3 |
)T |
|
|
|
Der Horizont liegt bei y = |
8,0 |
|
|
Der Nullpunkt bei ( |
4,0 |
1,3 |
)T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|